【利率】複利の効果は絶大。それでも定期預金に預けますか？

利率（金利）の推移について

皆さんは過去の金利水準をご存知ですか？

「昔は金利が良かった。」「郵便局で10年預けたら倍になった。」とか言われるのを聞いたことは無いでしょうか？

ゼロ金利が当たり前のような時代ですが、過去の金利を調べてみると信じられないような水準でした。

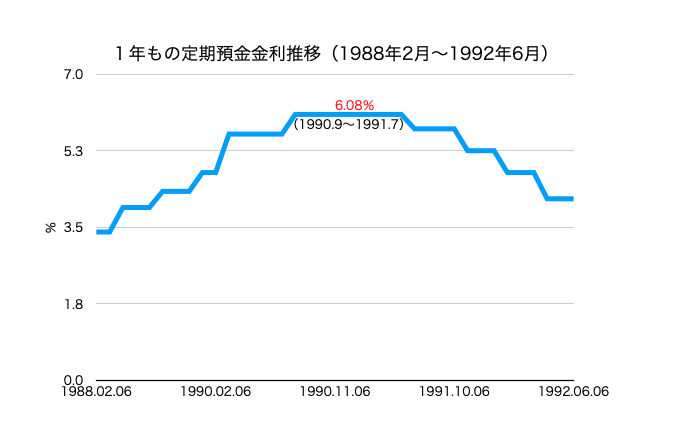
１年もの定期預金が1990年（平成2年）9月から翌年の7月まで6.08％だったんですね。

100万円を1年間預けると60,800円の利息がついたのですね･･･　そこから税金（20%）を差し引いても48,640円が貰える！

ちなみに、同じ１年もの定期預金の最新金利は0.003%（2021年2月3日：日本銀国金融機構局）となっています。

100万円を1年間預けると30円の利息が付きます･･･　そこから税金（20.315%）を差し引いて24円貰える💧

現役世代の私達にとっては寂しい時代ですね。

単利と複利の違い

話が逸れました。今回は利率の解説なので一般知識の解説をしていきます。

早速ですが、単利と複利の違いについて解説します。殆どの方が既に知っていることと思いますが、敢えて説明するのには理由があります。

それは複利の考え方がライフプランニングを行ううえで非常に重要だからです。

なので単純に単利と複利の意味を知っているだけでなく、活用の仕方を習得する必要があります。

まずは単利と複利の違いを見ていこうと思います。

単利

・１年分の金利　✗　運用期間

例）100万円を金利5%で運用して、毎年利息を貰って元本を再度運用する。

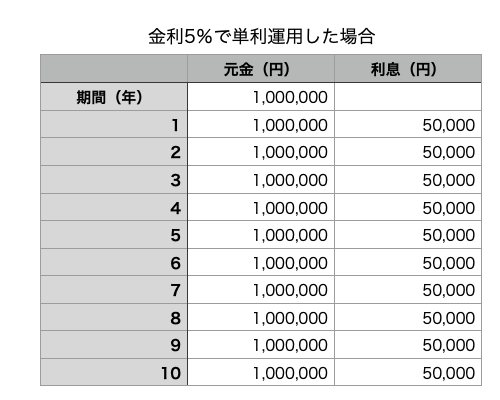
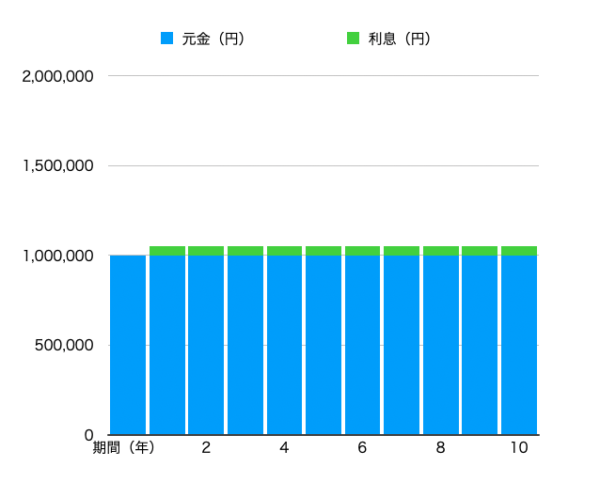
毎年利息を貰っているので、グラフの水色部分（元金）は変化しません。10年間貰える利息の合計は50,000円✗10年＝500,000円となります。

この場合、10年間運用して元金＋利息は1,000,000円＋500,000円＝1,500,000円となりました。（※税金は考慮していません）

複利

・１年分の金利を元金に繰り入れて、翌年の元金として繰り越していく。

例）100万円を金利5%で運用して、利息は貰わずに元金に加えて再度運用する。

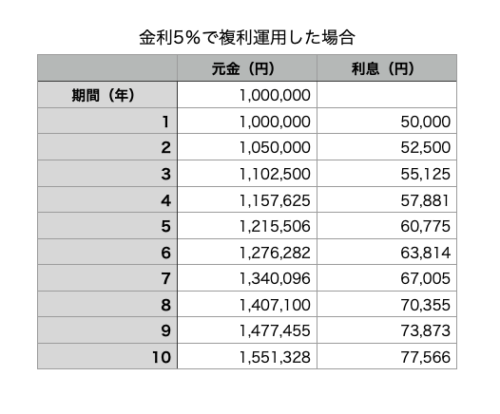
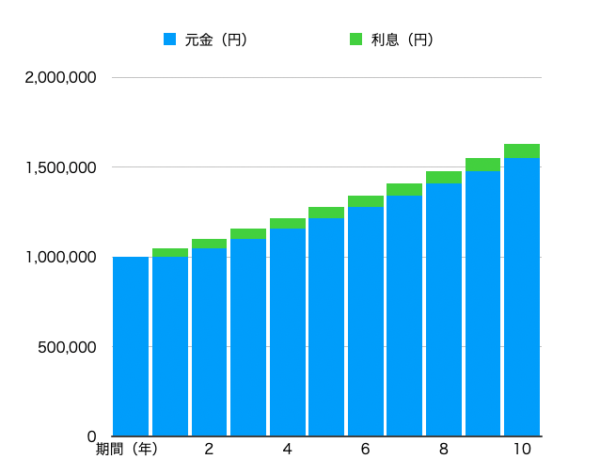
毎年利息を貰わずに元金に加えてますので、水色部分（元金）が増加していきます。増加した元金利息が発生するわけですので少しずつ利息も増えていきます。

この場合、10年間運用して元金＋利息は1,551,328円＋77,566円＝1,628,894円となります。（※税金は考慮していません）

上記のケースで単利と複利を比べると、複利のほうが128,894円も多く増えているのが分かります。

利息を元金に加えて運用する　→　元金が増える　→　増えた元金に対して利息が付く（利息に利息が付く）

雪だるま式に増えていくイメージですよね。

複利計算をベースにした活用方法

単利と複利の違いを理解して、次はその活用について説明していきたいと思います。少しややこしいと感じるかも知れませんが、とても重要なことですので頑張ってください。

公式に出てくるのは利率（年間）と期間（年数）だけです。

公式は全てｒ＝年利率、ｎ＝年数となっています。

終価係数

現在の額から将来の額を求めるときに使用します。

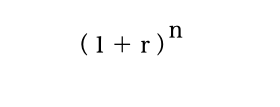
例えば、先程のケースと同様に100万円を5%の複利で3年運用したとしましょう。3年後の金額はこの公式で求めることができます。

そうすると、終価係数は（1＋0.05）の3乗で　1.05✗1.05✗1.05＝1.157625　となります。

3年後の元金＋利息は、1,000,000円✗1.157625＝1,157,625円となります。（前述の表でも確認してみてください。）

余談ですが、利率が7.2%で10年の複利運用すると終価係数は2.0042となりますので元金＋利息で倍になります。

では現行の１年もの定期預金の金利0.003%で100万円を10年間の複利運用をすると・・・

終価係数は1.0003となりますので、10年後には1,000,300円となります。（※税金は考慮していません）

いかに現行の金利で運用しても増えないのが分かりますよね。

現価係数

将来の額から現在の額を求める時に使用します。

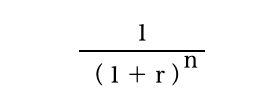
例えば、年利率5%で運用して10年後に100万円にしたいとき、今いくら必要かを求めることができます。

それでは現価係数を求めていきましょう。

まず分母から、（1+0.05）の10乗ですので　1.05✗1.05✗1.05✗1.05　･･･　＝1.6288942　となります。

なので現価係数は　1÷1.6288942＝0.6139134　となります。

最後に　1,000,000円✗0.6139134＝613,913円となり、これが回答となります。

年利率5%で複利運用できたら結構増えますよね。

子供の教育資金などに向けて資産を運用する場合に目安となるかもしれませんね。

例：子供が生まれたので18年後の大学費用を1,000万円貯めたい。仮に投資信託等で年利2%の運用が出来たとして今いくら必要か？

回答：現価係数は0.70015937となりますので、手元に7,001,594円必要となります。

年金終価係数

毎年の積立額から将来の元利合計を求める時に使用します。

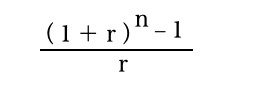
少しずつ複雑になっていますが大丈夫でしょうか？

これまでの公式では、ある程度まとまったお金がある時に参考になりますが、実際にはこつこつ積立をして資産を増やしていくことが多いと思います。

例えは、年利率5%で毎年50万円を10年間積み立てた場合、10年後にはいくらになるでしょう？

やや複雑な計算式ですので少しずつ行きましょう。

まず分子、（1＋0.05）10乗ー１ですので、（1.05✗1.05✗1.05✗1.05✗1.05✗1.05✗1.05✗1.05✗1.05✗1.05）ー1となり、0.6288942となります。

分母は0.05ですので、年金終価係数は　0.6288942÷0.05＝12.577884となります。

最終的な答えは500,000円✗12.577884＝6,288,942円となります。

金利を全く考慮しないと元金は50万円✗10年＝500万円ですので、このケースでは1,288,942円増えたことになります。

ちなみに現行の定期積金の金利水準0.005%で計算してみます。

年金終価係数は10.00225030となり、10年後には5,001,125円となります。　はい、1,125円増えます💧（くどいようですが税金は考慮していません）

減債基金係数

将来目的とする金額を貯めるために必要な毎年の積立額を求める時に使用します。

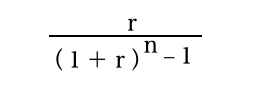
今度は逆のケースです。

例えば、年利2%で複利運用して10年後に500万円を貯めるのに毎年いくら積み立てればよいのかといったケースです。

今度は分母から計算していきます。（1+0.02）の10乗-1ですので、（1.02✗1.02✗1.02✗1.02･･･）−1で0.2189941となります。

分子が0.02ですので、減債基金係数は0.02÷0.2189941＝0.0913266となります。

なので、5,000,000円✗0.0913266＝456,633円が答えとなります。

毎年456,633円を積み立てて、2%の複利運用すると10年後には5,000,000円となります。

少し応用して、子供の教育資金として18年後に1,000万円を貯めたい場合、投資信託等で2%の複利運用が出来たと仮定しますと･･･

減債基金係数は0.04670210となり、10,000,000円✗0.04670210＝467,021円を毎年積み立てる必要があります。

金利がゼロの場合は、10,000,000円÷18年＝555,556円を毎年積み立てる必要があるので、やはり利率の力は大きいことが言えると思います。

年金現価係数

希望する年金額を受け取るために必要な年金原資を求める時に使用します。

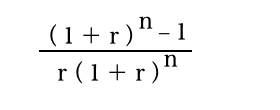
だいぶヤバくなって来ましたね（笑）ここから先は主に老後の話となります。

例えば、年利2%で複利運用しながら、毎年100万円の年金を10年間受け取るにはいくらの原資が必要なのかを計算する時に使用します。

分子：（1+0.02）の10乗-1なので、（1.02✗1.02✗1.02✗1.02･･･）-1＝0.2189941（①）

分母：0.02✗（1+0.02）の10乗ですので、0.02✗（1.02✗1.02✗1.02✗1.02・・・）＝0.0243798（②）

年金現価係数は、分子÷分母（①÷②）なので　0.2189941÷0.0243798＝8.9826044　となります。

最後に、1,000,000円✗8.9826044＝8,982,604円が答えとなります。

金利がゼロの場合は、100万円✗10年＝1,000万手元に必要ですが、複利運用ができると取り崩しながらも元金が増えているのが分かります。

資本回収係数

現在の額を年金原資として運用しながら受け取れる年金の額を求める時に使用します。また、借入額に対して利息を含めた毎月の返済額を求める時に使用します。

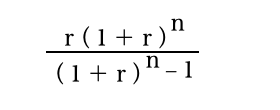
これが最後となります。

ケース１：1,000万円を年利2%で複利運用しながら10年にわたって年金として取り崩す場合、受け取れる年金の額を求める場合

分子：0.02✗（1+0.02）の10乗なので、　0.02✗（1.02✗1.02✗1.02✗1.02･･･）＝0.0243798（①）

分母：（1+0.02）の10乗-1なので、（1.02✗1.02✗1.02✗1.02･･･）-1＝0.2189941（②）

資本回収係数は、分子÷分母（①÷②）なので　0.0243798÷0.2189941＝0.1113262　となります。

最後に、10,000,000円✗0.113262＝1,113,262円が答えとなります。

金利がゼロの場合は、10,000,000円÷10年＝1,000,000円の年金ですので、2%で複利運用したら毎年113,262円余分に貰えることが分かります。

ケース２：2,000万円の住宅ローンを年利2%で借りて、15年返済する場合の年間返済額を求める場合（年1回払い）

分子：0.02✗（1+0.02）の15乗なので、0.02✗（1.02✗1.02✗1.02✗1.02･･･）＝0.0269173（①）

分母：（1+0.02）の15乗-1なので、（1.02✗1.02✗1.02✗1.02･･･）-1＝0.3458677（②）

資本回収係数は、分子÷分母（①÷②）なので　0.0269173÷0.3458677＝0.0778254　となります。

最後に、20,000,000円✗0.0778254＝1,556,508円が答えとなります。

まとめ

さて如何でしたでしょうか？

今回の内容はマニアック過ぎましたかね･･･💧個人的には、公式などは覚える必要はないと思います。ただ複利の考え方と効果をイメージとして覚えておく必要はあると感じています。

現行のゼロ金利では関係ないかも知れませんが、余剰資金を投資する際には、複利運用が基本となります。

また運用においては期間がいかに重要なのかが分かると思います。まとまったお金を運用するだけで無く、積み立ても期間が長くなるとそれだけ効果も大きくなるのです。

最後に、今回の記事で参考にしたサイトを紹介します。

「ややこしい計算式の説明をする前に、このサイトを紹介したら？」ってゆうツッコミは無しでお願いします。